- Basic
- Standard Compliant Channels
- $50
- Completely synergize resource taxing relationships via premier market
- 1 GB of space
- Support at $25/hour
- Sign Up
- Premium
- Standard Compliant Channels
- $100
- Completely synergize resource taxing relationships via premier market
- 10 GB of space
- Support at $15/hour
- Sign Up
- Platinum
- Standard Compliant Channels
- $250
- Completely synergize resource taxing relationships via premier market
- 30 GB of space
- Support at $5/hour
- Sign Up
Clasificación de los ángulos
De acuerdo con su medida los ángulos se clasifican en:
- Agudos: Son todos los ángulos con una amplitud menor de 90º.
- Rectos: Son los ángulos que miden, exactamente, 90º.
- Obtusos: Son los ángulos que miden más de 90º y menos de 180º
- Llanos: Son los ángulos que miden, exactamente 180º. A primera vista parecen una línea recta.
- Cóncavos: : Son los ángulos cuya amplitud es mayor de 180º y menor de 360º.
- Convexos: Son los ángulos que miden entre 0º y 180º.
- De giro o completos: Un ángulo de giro es el que mide, exactamente 360º.
De acuerdo con su suma los ángulos se clasifican en:
- complementarios: Dos ángulos son complementarios si suman 90º.
- Suplementarios: Dos ángulos son complementarios si suman 180º.
Ángulos ubicados en el plano cartesiano:
- Ángulo en posición estándar: Si ubicamos un ángulo de cualquier magnitud en un plano cartesiano, éste ángulo tiene su lado inicial en el eje de las “X” positivo y gira en cualquier sentido.
- Ángulos positivos y negativos: Cuando un ángulo en posición estándar o normal, gira en sentido contrario a las manecillas del reloj, se dice que es positivo o levógiro y cuando gira en sentido de las manecillas del reloj es negativo o dextrógiro.
- Ángulos del primer cuadrante: No importa en el sentido en que gire el lado móvil del ángulo; si este termina en el primer cuadrante, se dice que es un ángulo del primer cuadrante, si termina en el segundo, será un ángulo del segundo cuadrante y lo mismo aplica para los dos cuadrantes restantes.
- Ángulo cuadrantal: Si el lado terminal coincide con alguno de los ejes coordenados, entonces este ángulo se llama cuadrangular o cuadrantal.
- Ángulos coterminales: Cuando dos o más ángulos coinciden en su lado inicial y en su lado terminal, no importa en el sentido en el que giren, se llaman coterminales.
¿Qué es un ángulo?
En este artículo definimos el concepto de ángulo y la notación de ángulos.
Un ángulo es una abertura comprendida entre dos semirrectas que tienen un origen común llamado vértice. Las dos semirrectas se extienden indefinidamente por uno de sus extremos.
También podemos definir un ángulo como la porción del plano delimitada por dos semirrectas. La porción del plano dentro del ángulo se conoce como interior del ángulo y la otra porción se le denomina exterior del ángulo.
Los tres elementos principales de un ángulo son sus lados inicial y final (semirrectas que lo conforman), vértice (lugar donde estas se unen) y su apertura o amplitud (se mide en grados o en radianes).
Figura con las partes de un ángulo
Notación
Un ángulo se denota usualmente con tres letras mayúsculas, en donde la letra del centro marca el vértice y las otras dos señalan un punto en cada uno de los lados. Al hacer referencia al ángulo usamos la expresión, “el ángulo AOB” o “el ángulo BOA”. Es posible denotar un ángulo con la letra que marca el vértice siempre y cuando no haya otros ángulos con el mismo vértice en el diagrama.
Para evitar confusiones, cuando dos o más ángulos tienen el mismo vértice, se recomienda la utilización de números o letras griegas en el interior del ángulo , cerca de su vértice.
Al escribir, la palabra ángulo a menudo se reemplaza con el símbolo \(\angle\). Por ejemplo, en lugar de “el ángulo AOB” se puede escribir \(\angle AOB\).
Combinando términos semejantes
Un polinomio es una expresión algebraica formada por la suma monomios. El prefijo 'mono' significa 'uno', un monomio es una solo término. El prefijo 'poli' significa 'muchos'. Entonces la palabra polinomio se refiere a múltiples términos en una expresión. Las relaciones entre los términos pueden ser sumas o diferencias.
Ejemplos de polinomios sonn:
\[4x^3+8\] \[4x^4-2x^3-x-1 \] \[x^3 - 2x + 3\]Noción de media aritmética
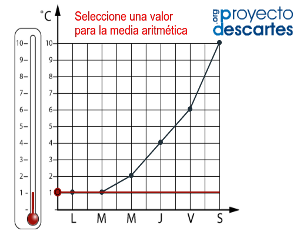
En la escena que sigue vas a distribuir las frecuencias y llegar a la noción de media aritmética.
Este recurso interactivo ha sido desarrollado con DescartesJS basándose en los materiales que la profesora Maria Antònia Canals ha ido elaborando y recopilando en su ejercicio docente y también con el gabinete GAMAR que dirige. Es una obra derivada del objeto desarrollado para el Ministerio de Educación español. El autor del objeto de aprendizaje interactivo es Diego Luis Feria Gómez, docente de la IED Marco Fidel Suárez (Barranquilla - Colombia).
Haga clic sobre la imagen para abrir la escena
Jerarquía de operaciones - Pedmas
Al momento de realizar operaciones aritméticas debemos respetar el orden de las operaciones (jerarquía de operaciones). Cuando una expresión aritmética involucra sumas, restas, multiplicaciones y/o divisiones el orden en el que debemos realizar las operaciones es el siguiente:
- Paréntesis
- Potencias
- Multiplicaciones, Divisiones
- Sumas, Restas
Utiliza las siguiente escena del Proyect Descartes para deducir y practicar la jerarquía de operaciones.
Esto significa que primero debemos resolver las operaciones que aparezcan entre paréntesis, luego las potencias, después las multiplicaciones y las divisiones (en el orden que queramos) y después las sumas y las restas (también en el orden que queramos. Si dentro de unos paréntesis aparecen otras operaciones se sigue la misma jerarquía.

Reducción de expresiones algebraicas
Utiliza la siguiente escena dinámica para simplificar una expresión algebraica reduciendo términos semejantes. La escena pertenece a Guillermo Tinoco Ojeda.
Valor numérico de una expresión algebraica
La escena que sigue realizada con el programa de geometría dinámica geogebra, pertenece a Javier Cayetano Rodríguez y permite practicar de manera ludica el tema de la evaluación de una expresión algebraica.
Utiliza esta escena para aprender y practicar el concepto de valor numérico de una expresión algebraica.
El modo juego consiste en resolver ejercicios de valor numérico.
- Hay que pulsar en un planeta con la solución (podrían llevarla varios).
- Cada respuesta correcta vale 1.5 puntos, pero los fallos penalizan 1 punto.
- ¡Cuidado! Aunque un número aparezca varias veces, no tiene por qué ser la solución.
Puedes alinear los planetas pulsando el botón ¡Alineados!, abajo a la izquierda. Además, pulsando en esa esquina puedes pausar/reanudar la animación.
Bienvenida
Hola a todos los que están leyendo esto!
Acá estoy de nuevo iniciando un nuevo proyecto con la esperanza de recopilar en un sólo lugar conteidos, vídeos, escenas dinámicas de geogebra y artículos de matemáticas, así que en caso de que estés ausente por enfermedad u otras razones, ¡puedes venir aquí!
Bienvenid@s entoces a mi blog, un espacio todavía en construcción creado como un punto de encuentro e intercambio entre quienes están interesados en temas vinculados a educación matemática y nuevas tecnologías.
Inicialmente aprovecharemos este espacio para compartir y publicar contenidos, e interactuar con la comunidad educativa de la IED Marco Fidel Suárez de Barranquilla y con todos aquellas personas interesadas en las matemáticas.
